This page collects interactive web applications I developed with Claude AI to illustrate key concepts in probability theory and statistical mechanics. The simulations are meant as pedagogical tools — for students, colleagues, or anyone interested in probability, typicality, the law of large numbers, irreversibility, and convergence to equilibrium. Each app runs in the browser and lets the user experiment with parameters to see how they affect statistical regularities.
My detailed views on probability and the foundations of statistical mechanics are laid out in the book Typicality Reasoning in Probability, Physics, and Metaphysics.
Web Applications
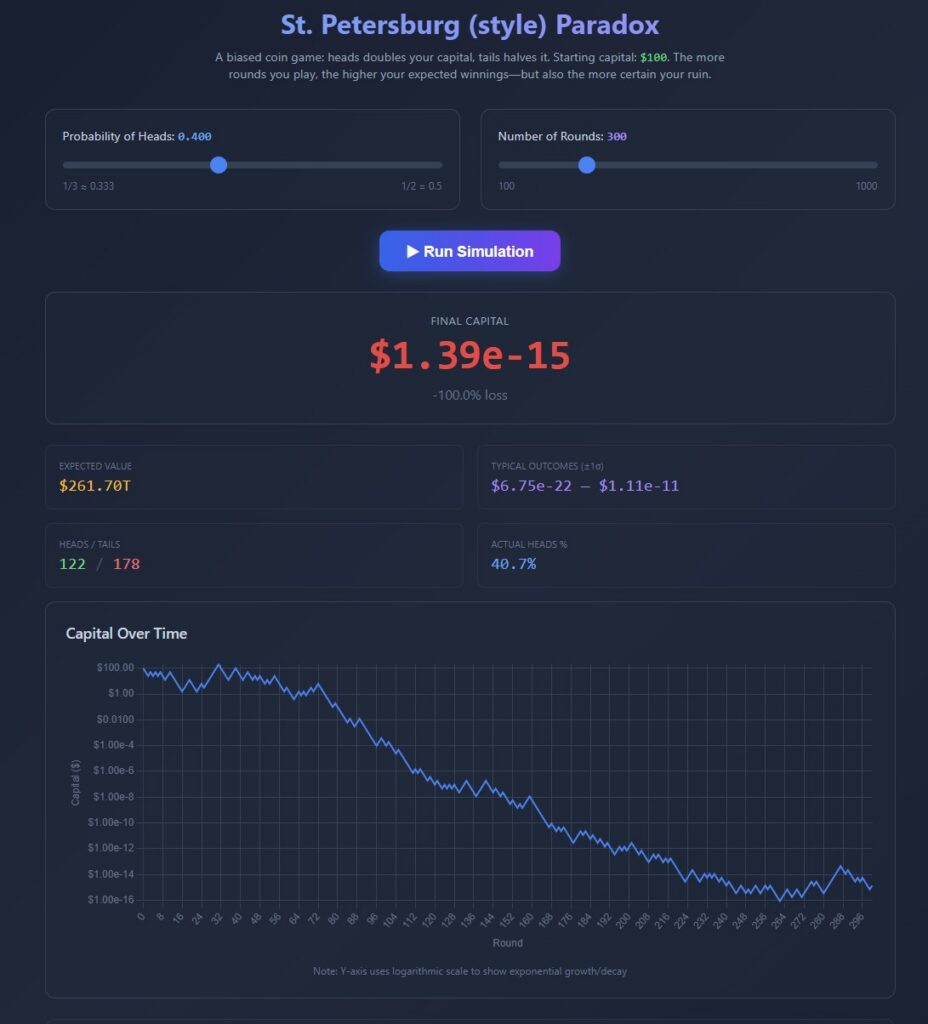
St. Petersburg-style Paradox: A simple game involving multiplicative betting, where theoretical expectation and typical outcomes diverge in dramatic fashion. With increasing number of rounds, the expected value goes to infinity, while the risk of ruin approaches 100%.
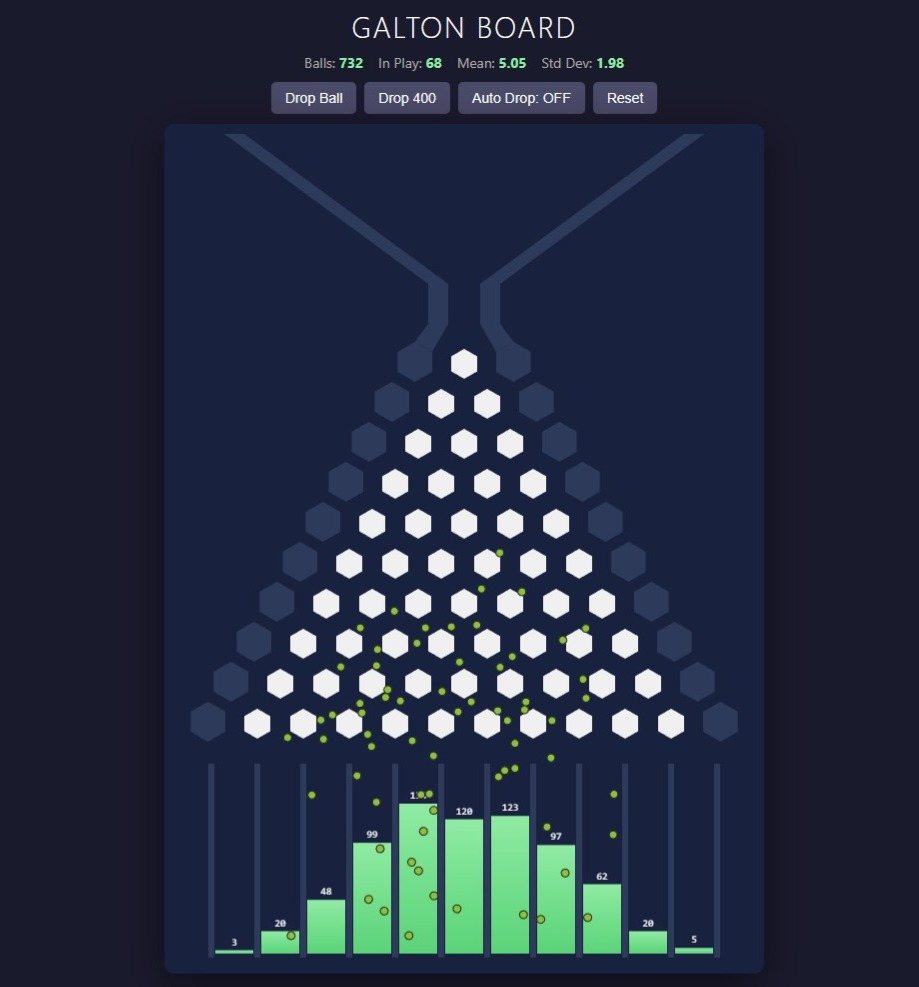
Galton Board: A classic demonstration of how deterministic but chaotic dynamics give rise to statistical regularities — here, a binomial distribution approximating a bell curve (as per the central limit theorem).
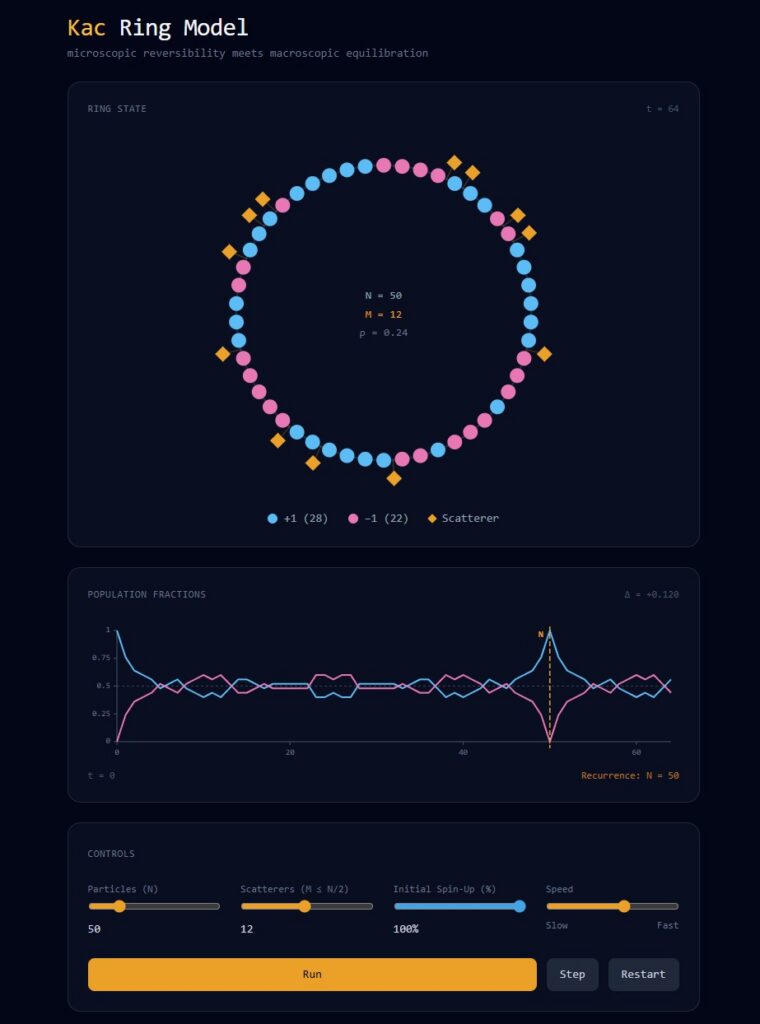
The Kac Ring: Mark Kac’s elegant model illustrating how deterministic, time-reversible microscopic dynamics produce macroscopic equilibration — and eventual Poincaré recurrence.
For a detailed discussion, I recommend this paper by Jean Bricmont.
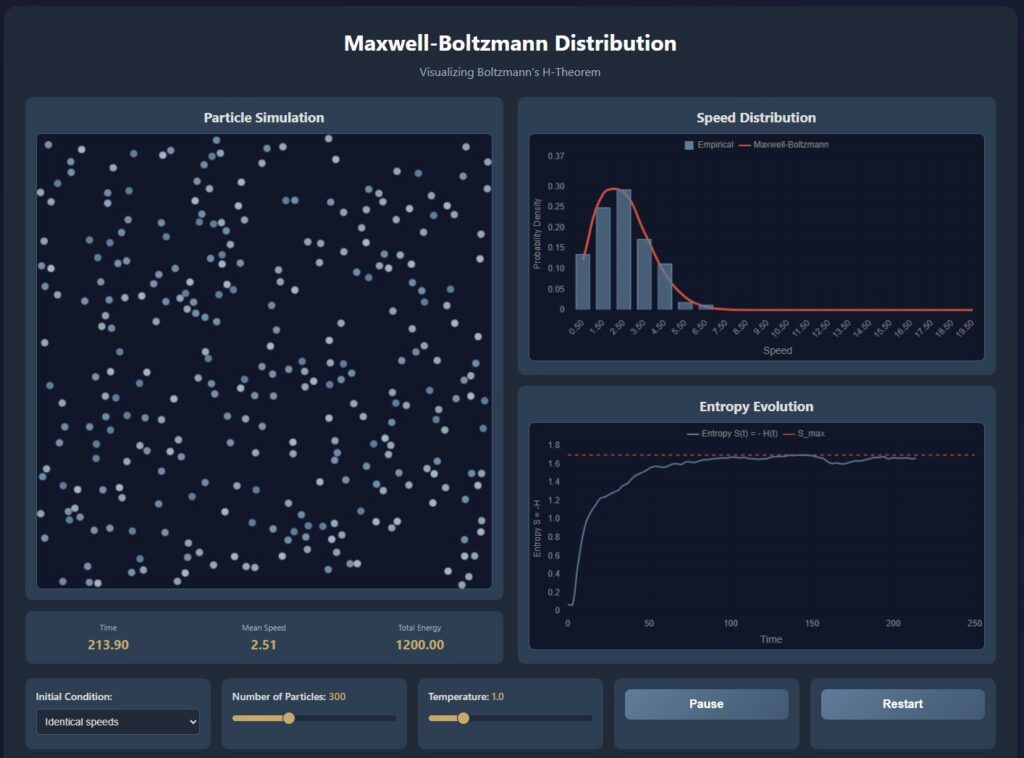
Maxwell-Boltzmann Distribution: A simulation of a two-dimensional hard disk gas, illustrating the H-theorem and convergence to a Maxwell-Boltzmann velocity distribution.
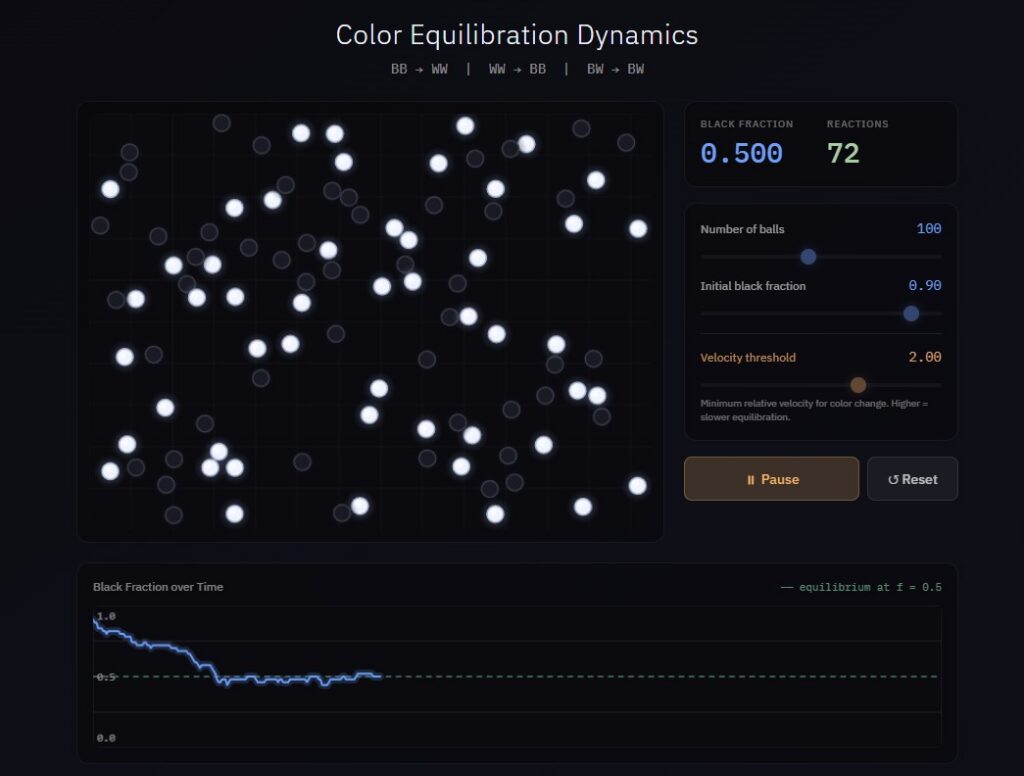
Color Equilibration: Black and white balls in a box that swap colors upon collision, illustrating spontaneous equilibration and detailed balance.